Tree

Tree

Node 와 Edge 로 이루어진 자료구조

Tree가 가져야 할 특징

• tree는 사이클이 존재해서는 안된다.
• 모든 노드는 자료형으로 표현이 가능하다.
• 루트에서 노드로 가는 경로는 유일해야한다.
• 노드의 갯수가 N이면 간선은 N-1을 가져야한다.

Graph와 Tree는 무슨 서로 싸이클의 유무로 판단한다.

트리의 순회 방식

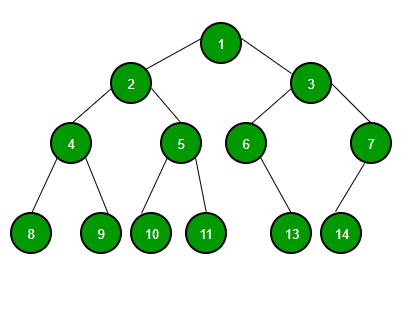
전위 순회

각 부모노드를 순차적으로 방문

$1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14$

중위 순회

왼쪽 하위 노드를 순차적으로 방문

$8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 -> 13 -> 3 → 14 → 7$

후위 순회

왼쪽 하위 노드부터 자식 노드를 순차적으로 방문

$8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 →6 → 14 → 7 → 3 → 1$

레벨 순회(level-order)

부모 노드부터 계층 별로 방문하는 방식

$1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14$

---

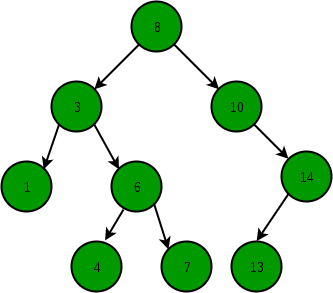
이진 탐색 트리

이진 탐색 + 연결 리스트

시간 복잡도

• 균등 트리 : 노드 개수가 N개일 때 $O(logN)$
• 편향 트리 : 노드 개수가 N개일 때 $O(N)$

이진 탐색 트리의 특징

• 각 노드는 자식이 2개 이하
• 각 노드의 왼쪽은 부모보다 작고 오른쪽은 부모 보다 크다.
• 중복된 노드는 없어야 한다.
  • 중복이 들어온다면 노드 안에 count 값으로 계산 한다.
  • 중복 처리 해버리면 성능 낮아짐
• 탐색은 언제나 중위 순회로 한다.
  • 정렬된 순서 로 읽을 수 있음!

이진 트리의 삭제

• 삽입은 뭐 쉽다.
• 삭제의 3가지 case
  • 자식 없는 노드 → 삭제
  • 자식이 1개인 경우 → 지워진 자리에 자식을 올린다.
  • 자식이 2개인 경우 → 가장 오른쪽 자식 노드를 찾아 가장 작은 값을 올린다.

---

Heap

완전 이진트리의 일부 최댓 값 최소 값의 빠른 탐색

Heap의 특징

• 반정렬 상태
• 힙을 저장하는 표준적인 자료구조는 배열
• 우선순위 큐를 위해 만들어진 자료구조
• 삭제 시에는?
  • 삭제 된 루트 노드의 힙의 마지막 노드를 끌어와서 재구성

---

AVL 트리

이진 트리 + 균형을 맞추자

AVL 트리의 특징

• 데이터 추가 후 + 회전 작업을 통해 트리의 높이를 조절

---

Red-Black Tree

하나의 노드가 하나의 Key값을 가진다.

• 모든 노드는 빨간색 검은색이다.
• Root와 Leaf는 검은색이다.
  • leaf는 NIL(노트의 끝)을 자식으로 가짐
• 빨간색 노드의 자식은 검은색이다.
• 모든 리프 노드에서 Black Depth는 같다.

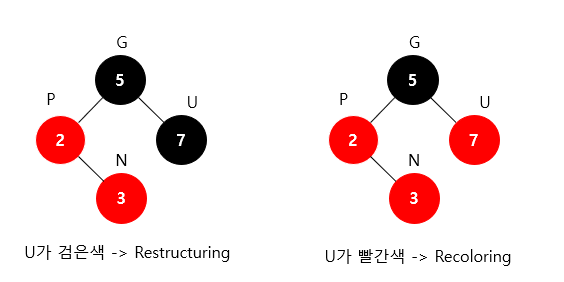
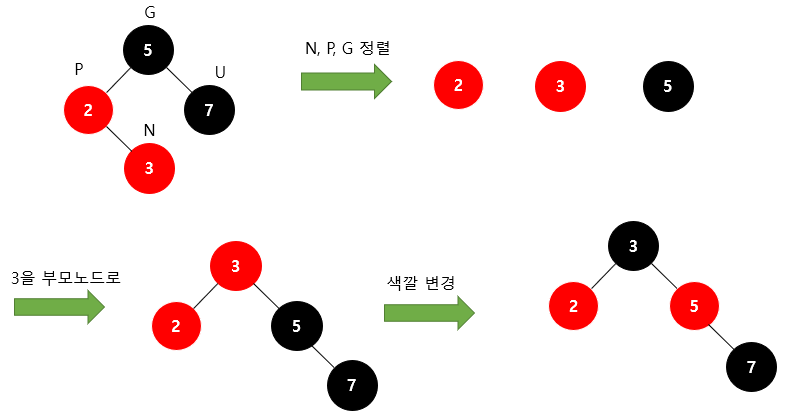
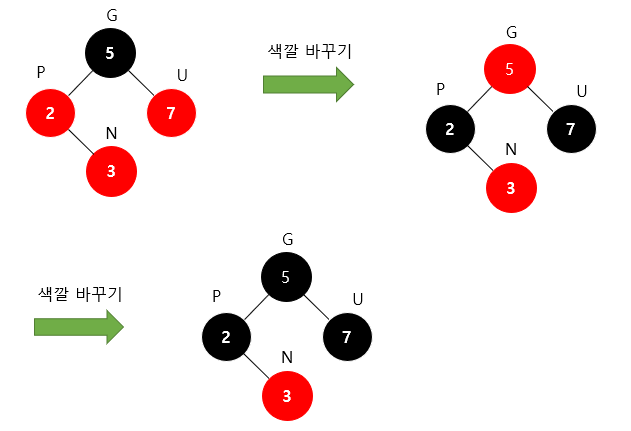
삽입

• 언제나 삽입은 Red로 정해진다.

• 그리고 Double Red를 해결하자!

  

새로 삽입할 노드를N(New), 부모 노드를P(Parent), 조상 노드를G(Grand Parent), 삼촌 노드를U(Uncle)

1. U가 검은색이라면 Restructuring 을 수행

   

   • N, P, G 를 재정렬 하고 노드 재 배치
   • 그리고 색깔을 설정

2. U가 빨간색이라면 Recoloring을 수행

   

→ 계속해서 Double Red가 발생한다면 계속해서 수행해야한다…

그래서 이거 왜 쓰는데?

• 삽입, 삭제, 검색에 있어 가장 일정한 시간을 보장

---

B Tree & B+ Tree

이진 트리는 자식이 2개, 균형이 맞지 않을 경우 효율 급감 모든 리프 노드들이 같은 레벨을 가질 수 있도록 조절한다.

B Tree

• DB, File System에서 널리 사용된다.
• 이진 트리에 더 많은 자식을 가지게 하자
• 트리의 균형을 자동으로 맞추게 하자
• 최대 M개의 자식을 가진다면 M차 B트리라고 한다.
• 자식을 탐색해 이진 탐색 트리처럼 찾고 자신의 범위에 들어간다. & 값을 찾아 push 한다.

B Tree의 특징

• 노드의 자료수가 N이면 자식 수는 N + 1이여야 한다.
• 루트 노드는 적어도 2개 이상의 자식을 가져야 한다.
• 중복 불가

B Tree의 SID

• 탐색
  • 자식을 탐색해 이진 탐색 트리처럼 찾고 자신의 범위에 들어간다. & 값을 찾아 push 한다.
• 삽입
  • 리프 노드가 가득 찾다면 중앙 값을 기준으로 분할을 수행 중앙 값 기준으로 좌우가 자식으로 변환
• 삭제
  • 자식 노드가 최소 갯수라면 부모와 형제를 merge 한다.

B+ Tree

• 기존의 B Tree에서 인덱스 역할만하는 비 단말 노드가 존재
• B Tree + 연결 리스트
• 기존의 B Tree는 모든 노드가 데이터가
  • 즉 Root나 상위 노드에서 끝날 수 있음
  • 하지만 B+ Tree노드들은 모든 데이터는 leaf Node에만 있다. 상위 Node들은 Key만 소유
  • 모든 삽입 삭제는 leaf Node에서만 이뤄진다.