5. er model

5. ER Model (23. 10. 26)

개체 관계 데이터 모델

• 데이터를 개체(Entity), 속성(Attribute), 관계(Relationship)로 나타내는 데이터 모델
• 실 세계를 개체(Entity)라 불리는 기본 객체들과 그 객체들 사이의 관계로 인식
• 데이터베이스의 전체 논리적 구조를 나타내는 조직의 스키마(Enterprise Schema)를 명시함으로써 데이터베이스를 쉽게 설계하도록 개발됨
• 실세계의 조직의 의미와 상호작용을 개념적 스키마로 나타내는데 매우 유용함

개체, 속성, 개체 집합

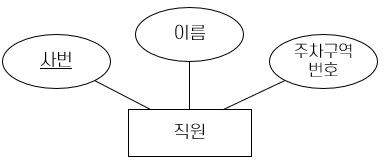
• 개체 (Entity)
  • 실제 세계에서 다른 객체와 구별되는 유, 무형의 사물
• 속성(Attribute)
  • 한 개체를 기술하기 위한 속성
  • 개체 집합에 속한 모든 개체들은 동일한 속성을 가짐
  • 가능한 집합을 Domain으로 설정, 식별을 위한 Key를 가진다.
• 개체 집합(Entity Set)
  • 개체들의 집합

관계, 관계 집합

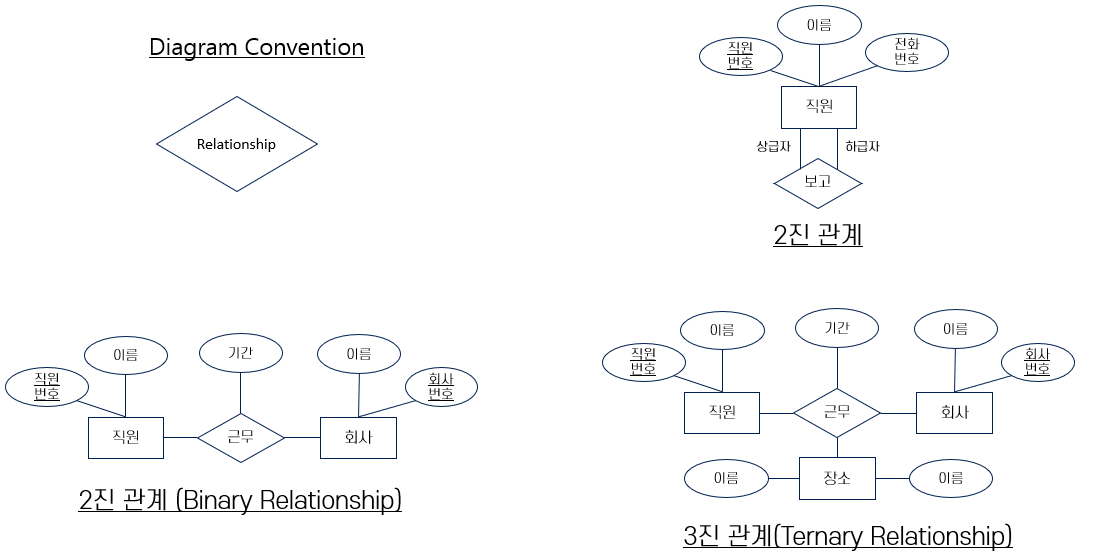
• 관계 (Relationship)
  • 여러 개체들 사이의 연관성
• 관계 집합(Relationship set)
  • 같은 유형의 관계들의 집합. n ≥ 2 개의 개체집합(중복 허용) 사이의 수학적 관계

• 만약 E1, E2… 들이 개체 집합일때 관계집합 R은

  ${(e1, e2,… en)

  e1 ∈ E1 … en ∈ En}$

  의 부분 집합이다. 여기서 e1, e2… 는 관계

개체 집합 → 관계 집합

• 개체 집합은 하나의 릴레이션으로 매핑

사번	이름	주차구역번호
1	이순신	47
2	홍길동	16

이러한 직원 테이블의 DDL 은 다음과 같다 .

CREATE TABLE 직원 (
	사번	        int,
	이름	        varchar(10)m
	주차구역번호	int,

	CONSTRAINT pk_employee PRIMARY KEY(사번)
)

• 이러한 둘 이상의 개체과 관련성을 말한다면 이를 관계로 연계하고 합하는 것을 관계 집합 이라고 한다.
• 만약 관계로 매핑한다면?

• 개체 집합처럼 관계집합도 관계로 매핑된다.
  • 참여하는 각 개체 집합의 기본키 속성 (외래 키 필드의 자격)
  • 관계 집합 자체의 설명형 속성

• DDL

    CREATE TABLE 근무 (
    	사번 int,
    	부서번호 int,
    	근무시작일 date,
      
    	CONSTRAINT pk_근무 PRIMARY KEY(사번, 부서번호),
    	CONSTRAINT fk_근무_직원 FOREIGN KEY(사번) REFERENCES 직원(사번),
    	CONSTRAINT fk_근무_부서 FOREIGN KEY(부서번호) REFERENCS 부서(부서번호)
    )
  

    CREATE TABLE 보고 (
    	상급자_사번	int,
    	하급자_사번	int,
    	CONSTRAINT pk_보고 PRIMARY KEY(상급자_사번, 하급자_사번),
    	CONSTRAINT fk_보고_상급자 FOREIGN KEY(상급자_사번) REFERENCES 직원(사번),
    	CONSTRAINT fk_보고_하급자 FOREIGN KEY(하급자_사번) REFERENCES 직원(사번)
    )
  

대응 수

• 참여 제약 조건(Participation Constraint)을 이루는 관계 비율
• 대응 수(Mapping Cardinality) 또는 수비율(Cardinality Ratio)

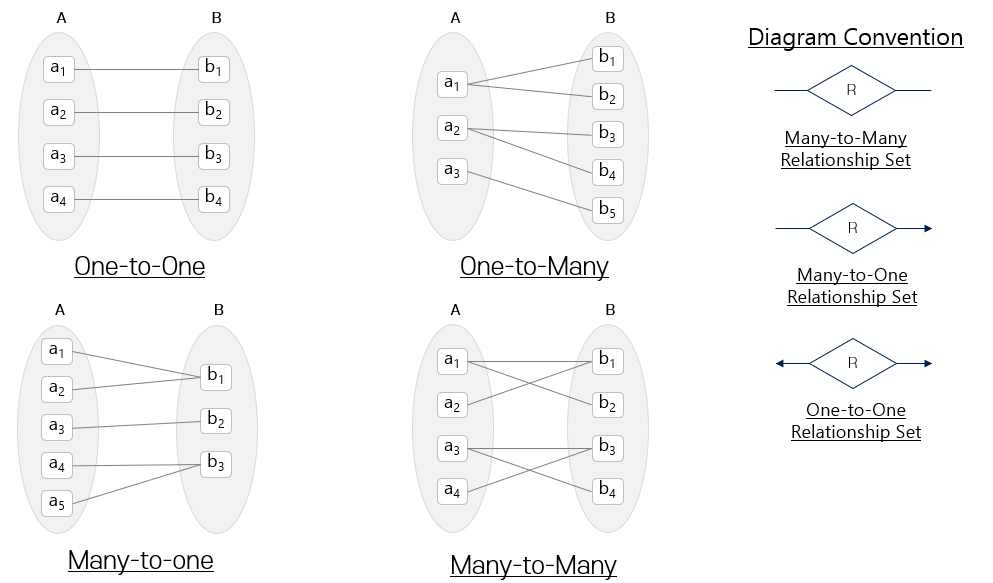
  • One-to-One

    A의 한 개체는 B의 한 개체와 연관을 가지고 B의 한 개체는 A의 한 개체 연관을 가진다.

  • One-to-Many

    A의 한 개체는 임의의 수 (0 또는 그 이상)의 B 개체와 연관을 가진다. 그러나 B의 개체는 A의 한 개체만 연관을 가진다.

  • Many-to-One

    A의 한 개체는 B의 한 개체와 연관을 갖는다. 그러나 B의 개체는 A의 임의의 수 (0또는 그 이상)의 개체와 연관을 갖는다.

  • Many-to-Many

    A의 한 개체는 임의의 수(0 또는 그 이상)의 B 개체와 연관을 갖고 B의 한 개체도 임의의 수 (0 또는 그 이상)의 A 개체와 연관을 갖는다 s

• 수 비율이라도 불리며 관계집합을 통하여 다른 개체와 관련 될 수 있는 개체의 수를 나타낸다.

키 제약 조건

• 키 제약 조건에 따라 대응수가 정해짐

  

  • 각 부서에 한명의 부서장이 있다 → 키 제약조건
  • 한 직원이 부서장으로 여러 부서와 관련있을 수 있지만, 각 부서는 한명의 직원만 부서장으로 관련되는것 → 일대다
  • 한명의 직원이 여러 부서 근무 가능, 부서에는 여러명의 직원이 근무 가능 → 다대다

약 개체 집합

• 키가 존재하지 않는 개체집합
  • 자신의 일부 속성과 다른 개체의 Primary Key를 조합하여야 유일하게 식별 됨
  • 다른 개체를 식별 소유자(Identity Owner)라고 함
• 다음 조건들을 만족할 때 성립
  • 식별 소유자와 약 개제 집합 사이에는 One-to-Many 관계 집합이 성립
  • 약 개체 집합은 식별 관계집합에 전체적으로 참여하여야 함
  • 소유자 개체에 대해 약 개제 하나를 유일하게 식별해 주는 속성 집합을 약 개체집합에 대한 구별자(discriminator) 또는 부분 키(Partial Key)라고 함
• 예를 들어 직원들에 대한 가족에 대한 보험증권 구매의 경우 피 부양자를 약 개체 집합 이라고 부른다.
• 자기 자신의 일부 속성과 다른 개체의 기본키를 조합해야만 식별 가능한 것 이때 사용되는 다른 개체를 식별 소유자 라고 불린다. 그리고 자기 자신의 일부 속성을 부분 키 라고 불린다.

Specialization와 Generalization

• 하나의 개체 집합은 집합내의 다른 개체들과 구분되는 개체들의 하위집합을 가질 수 있음
  • 개체 집합 내의 어떤 부분집합은 개체 집합내의 모든 개체들과 공유되지 않는 속성들을 가질 수 있음
  • 개체 집합에 속한 세부 개체들을 세부 부류(subclass)로 분류
• 포함 제약 조건(Inclusion Constraint)

  • 중첩 제약 조건(Overlap Constraints)

    두 서브 클래스에 같은 개체가 포함될 수 있는가를 결정

  • 포괄 제약 조건(Covering Constraints)

    서브 클래스의 모든 개체를 모으면 수퍼 클래스의 모든 개체가 되어야 하는가를 결정

• ISA 계층 구조 → 자바의 상속과 비슷함
• 만약 일반 직원 개체와 시간제 직원 개체를 만든다면 일반 개체에 시간제 직원을 자식으로 일반적인 직원의 정보와 시간제 직원 개체만의 특성을 갖는다. (상속) → 임원도 마찬가지지
• 하지만 Java 와 다른 포함 제약조건 이 따른다.

개념적 설계 고려사항

ER 모델을 이용한 개념적 설계

• ER 다이어그램 개발 과정은 선택의 연속
• ER 다이어그램은 데이터를 최대한 비슷하게 설명할 뿐, 모든 의미를 다 표현할 수 없음
• ER 모델링은 스키마 설계에 대한 완벽한 방법이 아님

개체 or 속성

• 속성으로 모델링 하는 경우
• 한 개체가 속성을 단일 값으로 가지는 경우
• 요구 사항에서, 수직, 수평적으로 분리될 수 없는 값인 경우
• 개체로 모델링하는 경우
• 한 개체가 여러 개의 값을 가지는 경우

• ER 다이어그램에서 주소의 구조를 표현해야 하는 경우

• 어떤 개체 집합에 있어 속성으로 표현할 것인지 관계집합으로 표현할 것인지는 요구사항에 따라 달라진다.
• 만약 주소를 하나의 개체 집합으로 만들고 관계를 할 수도 있다. → 만약 직원들이 여러 주소를 가지고 있을 경우
  • 이럴 경우 주소에 대한 질의를 작성하기도 가능하다.

개체 or 관계

• 개체로 모델링하는 경우
  • 관계가 관계로 생성되는 한 개체에 국한되는 속성을 가짐
  • A 개체집합의 개체가 정확히 B 개체집합의 한 개체에만 해당
• 관계로 모델링 하는 경우
  • 관계집합에서 중복이 발생하는 경우
  • 두 개체 사이에 일어나는 동작을 기술하는 경우